Đệ Quy (Recursion)

"Trong lập trình, đệ quy (recursion) là một kỹ thuật mà một phương thức tự gọi lại chính nó để giải quyết một bài toán bằng cách chia nhỏ thành các bài toán con. Đệ quy rất hữu ích khi làm việc với các cấu trúc phân cấp như cây hoặc khi cần lặp lại một công việc dựa trên điều kiện nhất định. Dưới đây là những điều cơ bản bạn cần biết về đệ quy trong Java:"

Giải thích từ đệ quy (Recursion)

↳ Tiền tố "Đệ": có nghĩa là "thứ hai", "sau", "kế tiếp". Trong trường hợp này, nó thể hiện mối quan hệ lặp lại, khi một hành động (ví dụ: gọi một phương thức) xảy ra sau chính nó.

↳ Gốc "quy": có nghĩa là "quy tắc", "lề luật", "phương pháp". Nó ám chỉ việc thiết lập một quy tắc lặp lại theo một cấu trúc nhất định.

Ưu điểm của đệ quy (Recursion)

↳ Đệ quy giúp giải quyết các vấn đề phức tạp bằng cách chia nhỏ chúng thành các vấn đề con đơn giản hơn. Điều này thường dẫn đến mã nguồn ngắn gọn và dễ hiểu.

↳ Đối với các bài toán có cấu trúc tự tương đồng (recursive structures) như cây và đồ thị, đệ quy thường cho phép bạn viết mã rõ ràng và dễ bảo trì hơn.

↳ Đệ quy có thể thay thế các vòng lặp trong một số trường hợp, giúp mã nguồn dễ đọc hơn và tập trung vào cấu trúc logic của thuật toán.

Nhược điểm của đệ quy (Recursion)

↳ Mỗi cuộc gọi đệ quy tạo ra một khung ngăn xếp mới, dẫn đến việc tiêu tốn bộ nhớ lớn. Điều này có thể gây ra lỗi tràn ngăn xếp (stack overflow) nếu độ sâu đệ quy quá lớn.

↳ Đệ quy thường có tiêu tốn nhiều bộ hơn so với vòng lặp do việc tạo và hủy bỏ các khung ngăn xếp. Điều này có thể làm giảm hiệu suất của chương trình, đặc biệt là trong các ứng dụng yêu cầu hiệu suất cao.

↳ Việc hiểu và gỡ lỗi các chương trình đệ quy có thể phức tạp hơn so với các chương trình sử dụng vòng lặp.

↳ Nếu không có điều kiện dừng đúng đắn hoặc nếu điều kiện dừng không bao giờ đạt được, chương trình có thể gây ra lỗi tràn ngăn xếp (stack overflow), dẫn đến việc chương trình bị ngừng hoạt động.

Cấu trúc của một hàm đệ quy

↳ Trường hợp cơ sở (base case): Điều kiện dừng của đệ quy, khi điều kiện này được thỏa mãn, hàm sẽ trả về kết quả mà không gọi lại chính nó.

↳ Bước đệ quy (recursive case): Hàm gọi lại chính nó với một tham số đầu vào nhỏ hơn so với lần gọi trước.

Cú pháp chung của một hàm đệ quy:

kiểu_trả_về tên_hàm(các_tham_số) {
    // Trường hợp cơ sở (base case):
    if (điều_kiện_dừng) {
        return kết_quả;
    }
    // Bước đệ quy (recursive case):
    return biểu_thức_gọi_lại_hàm_với_tham_số_mới;
}

Giải thích:

↳ kiểu_trả_về Kiểu dữ liệu mà hàm sẽ trả về.

↳ tên_hàm: Tên của hàm đệ quy.

↳ các_tham_số: Các giá trị truyền vào hàm.

↳ Trường hợp cơ sở: Đây là điều kiện để dừng đệ quy. Khi điều kiện này được thỏa mãn, hàm sẽ trả về kết quả trực tiếp mà không gọi lại chính nó.

↳ Bước đệ quy: Ở đây, hàm gọi lại chính nó với các tham số mới, thường là một phiên bản đơn giản hơn của bài toán ban đầu.

Ví dụ 1: Hàm đệ quy trong Java mà không có điều kiện dừng

Một hàm đệ quy mà không có điều kiện dừng sẽ tạo ra một vòng lặp vô hạn.

public class Example {
    public static void main(String[] args) {
        DeQuyVoHan();
    }
    public static void DeQuyVoHan() {
        System.out.println("Đây là cuộc gọi đệ quy vô hạn - bấm Ctrl+C để dừng.");
        DeQuyVoHan(); // Gọi đệ quy không có điều kiện dừng
    }
}

Trong ví dụ trên, Chương trình sẽ liên tục in dòng chữ " Đây là cuộc gọi đệ quy vô hạn - bấm Ctrl+C để dừng." cho đến khi xảy ra lỗi StackOverflowError. Vì mỗi lần gọi hàm DeQuyVoHan, một khung mới được tạo trên ngăn xếp gọi hàm, và ngăn xếp này có giới hạn. Khi ngăn xếp đầy, lỗi tràn ngăn xếp (StackOverflowError) sẽ xảy ra.

Ví dụ 2: Hàm đệ quy trong Java có điều kiện dừng

Để tránh vòng lặp vô hạn, bạn cần một điều kiện dừng. Điều kiện dừng là một kiểm tra logic để xác định khi nào hàm đệ quy không nên gọi lại chính nó nữa.

public class Example {
    public static void main(String[] args) {
        DeQuy(5);
    }

    public static void DeQuy(int n) {
        if (n <= 0) {
            System.out.println("Điều kiện dừng: n = " + n);
            return;
        }
        System.out.println("Bước 1: n = " + n);
        DeQuy(n - 1); 
    }
}

Trong ví dụ này, hàm DeQuy sẽ dừng lại khi n nhỏ hơn hoặc bằng 0, ngăn chặn vòng lặp vô hạn.

Ví dụ 3: Hàm đệ quy với một điều kiện dừng và hai lời gọi đệ quy

Nếu bạn có một hàm đệ quy với một điều kiện dừng và hai bước gọi đệ quy, thứ tự gọi sẽ tuân theo một mô hình cụ thể dựa trên cách mà các lời gọi đệ quy được đặt trong mã. Điều này thường được gọi là đệ quy cây (recursive tree).

public class Example {
    public static void main(String[] args) {
        DeQuy(3);
    }

    public static void DeQuy(int n) {
        if (n <= 0) {
            System.out.println("Điều kiện dừng: n = " + n);
            return;
        }
        System.out.println("Bước 1: n = " + n);
        DeQuy(n - 1); // Bước gọi đệ quy 1
        
        System.out.println("Bước 2: n = " + n);
        DeQuy(n - 2); // Bước gọi đệ quy 2
    }
}

Khi bạn có một hàm đệ quy với một điều kiện dừng và hai bước gọi đệ quy, thứ tự gọi sẽ là từ trên xuống dưới trong cây đệ quy. Mỗi lần hàm gọi chính nó, nó sẽ thực hiện bước đầu tiên và gọi đệ quy lần đầu, sau đó thực hiện bước thứ hai và gọi đệ quy lần thứ hai. Điều này tiếp tục cho đến khi điều kiện dừng được thoả mãn.

Mô hình đệ quy và thứ tự gọi

Chúng ta sẽ theo dõi thứ tự các lời gọi và giá trị của n trong mỗi bước. Sơ đồ cây đệ quy sẽ giúp minh họa rõ ràng hơn.

Ví dụ 4: Phương thức đệ quy có thể thực hiện một hành động cụ thể in ra thông tin và không cần kiểu dữ liệu trả về:

public class Example {
    
    // Phương thức đệ quy không trả về giá trị (void)
    public void printNumbers(int n) {
        if (n <= 0) {
            return; // Điều kiện dừng
        }
        System.out.println(n);
        printNumbers(n - 1); // Cuộc gọi đệ quy
    }

    public static void main(String[] args) {
        Example example = new Example();
        example.printNumbers(5);
    }
}

Cách thức hoạt động đệ quy của ví dụ trên:

Gọi hàm

↳ Khi bạn gọi example.printNumbers(5), chương trình bắt đầu thực thi hàm printNumbers với tham số n bằng 5.

Điều kiện dừng (Base case)

↳ Mỗi phương thức đệ quy phải có một điều kiện dừng để ngăn việc đệ quy vô hạn.

↳ Trong phương thức printNumbers, điều kiện dừng là if (n ≤ 0). Khi n nhỏ hơn hoặc bằng 0, phương thức sẽ trả về và không thực hiện các bước đệ quy tiếp theo.

In ra giá trị và gọi đệ quy

↳ Nếu n lớn hơn 0, phương thức sẽ in giá trị n ra màn hình bằng System.out.println(n).

↳ Sau đó, phương thức gọi chính nó với giá trị n - 1 (printNumbers(n - 1)). Đây là bước đệ quy, nơi phương thức tự gọi lại với một giá trị khác.

Ví dụ minh họa với n = 5, nó thực hiện các bước sau:

↳ Gọi printNumbers(5):

↳ In ra 5.

↳ Gọi printNumbers(4).

↳ Gọi printNumbers(4):

↳ In ra 4.

↳ Gọi printNumbers(3).

↳ Gọi printNumbers(3):

↳ In ra 3.

↳ Gọi printNumbers(2).

↳ Gọi printNumbers(2):

↳ In ra 2.

↳ Gọi printNumbers(1).

↳ Gọi printNumbers(1):

↳ In ra 1.

↳ Gọi printNumbers(0).

↳ Gọi printNumbers(0):

↳ Điều kiện dừng n ≤ 0 là đúng.

Phương thức trả về mà không thực hiện bất kỳ hành động nào thêm.

Quá trình quay lại (Unwinding)

↳ Sau khi điều kiện dừng được đạt, phương thức printNumbers(0) kết thúc và quay lại phương thức gọi trước đó, tức là printNumbers(1). Tương tự, phương thức printNumbers(1) quay lại printNumbers(2), và quá trình này tiếp tục cho đến khi tất cả các cuộc gọi đệ quy quay lại phương thức main.

Kết quả cuối

↳ Kết quả cuối cùng là các số từ 5 đến 1 được in ra theo thứ tự giảm dần.

Ví dụ 5: Sử dụng đệ quy để tính giai thừa và có kiểu trả về dữ liệu

public class FactorialExample {

    // Phương thức tính giai thừa bằng đệ quy
    public static int factorial(int n) {
        if (n == 0) {
            return 1; // Điều kiện dừng
        } else {
            return n * factorial(n - 1); // Cuộc gọi đệ quy
        }
    }

    public static void main(String[] args) {
        int number = 5;
        System.out.println("Giai thừa của " + number + " là " + factorial(number));
    }
}
}

Cách thức hoạt động của chương trình trên:

Gọi hàm

↳ Khi bạn gọi number = 5, chương trình bắt đầu thực thi với tham số n bằng 5.

Điều Kiện Dừng (Base case)

↳ Điều kiện dừng trong phương thức factorial là if (n == 0). Khi n bằng 0, phương thức trả về 1 vì giai thừa của 0 là 1 (theo định nghĩa toán học).

↳ Đây là điều kiện để kết thúc đệ quy và không thực hiện thêm các cuộc gọi đệ quy.

In ra giá trị và gọi đệ quy

↳ Nếu n không bằng 0, phương thức thực hiện return n * factorial(n - 1).

↳ Phương thức gọi chính nó với giá trị n - 1, tức là giảm giá trị của n và tính giai thừa cho giá trị giảm đó.

Ví dụ minh họa với number = 5, nó thực hiện các bước sau:

↳ Gọi factorial(5): Không bằng 0, nên phương thức thực hiện return 5 * factorial(4).

↳ Gọi factorial(4): Không bằng 0, nên phương thức thực hiện return 4 * factorial(3).

↳ Gọi factorial(3): Không bằng 0, nên phương thức thực hiện return 3 * factorial(2).

↳ Gọi factorial(2): Không bằng 0, nên phương thức thực hiện return 2 * factorial(1).

↳ Gọi factorial(1): Không bằng 0, nên phương thức thực hiện return 1 * factorial(0).

↳ Gọi factorial(0): n bằng 0, nên phương thức trả về 1.

Quá trình quay lại (Unwinding)

Sau khi điều kiện dừng được đạt, các cuộc gọi đệ quy bắt đầu quay lại:

↳ factorial(1) nhận được giá trị từ factorial(0):

↳ return 1 * 1 = 1.

↳ factorial(2) nhận được giá trị từ factorial(1):

↳ return 2 * 1 = 2.

↳ factorial(3) nhận được giá trị từ factorial(2):

↳ return 3 * 2 = 6.

↳ factorial(4) nhận được giá trị từ factorial(3):

↳ return 4 * 6 = 24.

↳ factorial(5) nhận được giá trị từ factorial(4):

↳ return 5 * 24 = 120.

Kết quả cuối

Kết quả cuối cùng của factorial(5) là 120

Ví dụ 6: Sử dụng đệ quy để tính dãy số Fibinacci

Dãy Fibonacci là một dãy số vô hạn các số tự nhiên bắt đầu bằng 0 và 1, các số tiếp theo được tính bằng tổng của hai số liền trước đó.

Công thức:

F(0) = 0

F(1) = 1

F(n) = F(n-1) + F(n-2) với n ≥ 2

public class FibonacciSeries {

    // Biến tĩnh để giữ giá trị của các số Fibonacci
    static int F0 = 0, F1 = 1, Fn;

    // Phương thức tính số Fibonacci bằng đệ quy
    public static int fibonacci(int count) {
        if (count == 0) {
            return F0; // Điều kiện dừng: Fibonacci(0) = 0
        } else if (count == 1) {
            return F1; // Điều kiện dừng: Fibonacci(1) = 1
        } else {
            // Cuộc gọi đệ quy và cập nhật biến tĩnh
            Fn = fibonacci(count - 1) + fibonacci(count - 2);
            return Fn;
        }
    }

    public static void main(String[] args) {
        int count = 5; // Số lượng số Fibonacci cần in ra

        // In ra số Fibonacci thứ count
        System.out.println("Số Fibonacci thứ " + count + " là " + fibonacci(count));

        // In ra dãy số Fibonacci từ 0 đến count
        System.out.println("Dãy số Fibonacci:");

        // Sử dụng vòng lặp để in ra các số Fibonacci từ 0 đến count
        for (int i = 0; i <= count; i++) {
            System.out.print(fibonacci(i) + " ");
        }
    }
}

Phân tích chi tiết cách nó hoạt động nhé.

Biến tĩnh F0, F1 và Fn:

↳ Mục đích: Lưu trữ hai số Fibonacci đầu tiên để làm điều kiện dừng cho đệ quy.

↳ Lý do dùng biến tĩnh:Để giữ giá trị của F0 F1 và Fn trong suốt quá trình thực thi chương trình, tránh tính toán lại.

Phương thức fibonacci(int count):

↳ Điều kiện dừng:

↳ Nếu count bằng 0, hàm trả về F0 (bằng 0).

↳ Nếu count bằng 1, hàm trả về F1 (bằng 1).

↳ Bước đệ quy:

↳ Nếu count lớn hơn 1, hàm sẽ gọi chính nó hai lần với tham số count - 1 và count - 2, sau đó cộng hai kết quả lại. Điều này tuân theo công thức tính Fibonacci: F(n) = F(n-1) + F(n-2).

Phương thức main:

↳ Gọi hàm fibonacci: Gọi hàm fibonacci để tính số Fibonacci thứ count và in ra kết quả.

↳ In dãy số: Sử dụng vòng lặp for để in ra các số Fibonacci từ 0 đến count.

Cách thức hoạt động chi tiết. Ví dụ minh họa với fibonacci(5). Quá trình thực hiện sẽ như sau:

↳ Tính fibonacci(5): fibonacci(5) = fibonacci(4) + fibonacci(3)

↳ Tính fibonacci(4): ffibonacci(4) = fibonacci(3) + fibonacci(2)

↳ Tính fibonacci(3): fibonacci(3) = fibonacci(2) + fibonacci(1)

↳ Tính fibonacci(2): fibonacci(2) = fibonacci(1) + fibonacci(0)

↳ Tính fibonacci(2): fibonacci(1): Trả về 1, fibonacci(0): Trả về 0.

Quá trình quay lại (Unwinding)

Sau khi điều kiện dừng được đạt, các cuộc gọi đệ quy bắt đầu quay lại:

↳ Tính fibonacci(2) từ điều kiện dừng:

↳ fibonacci(2) = fibonacci(1) + fibonacci(0) = 1 + 0 = 1.

↳ Tính fibonacci(3) từ kết quả fibonacci(2) và điều kiện dừng là fibonacci(1)

↳ fibonacci(3) = fibonacci(2) + fibonacci(1) = 1 + 1 =2

↳ Tính fibonacci(4) từ kết quả fibonacci(3) và fibonacci(2)

↳ fibonacci(4) = fibonacci(3) + fibonacci(2) = 2 + 1 =3

↳ Tính fibonacci(5) từ kết quả fibonacci(4) và fibonacci(3)

↳ fibonacci(5) = fibonacci(4) + fibonacci(3) = 3 + 2 = 5

Kết Quả Cuối

Kết quả cuối cùng của Số Fibonacci thứ 5 là 5, vì số Fibonacci thứ 5 là 5.

Vòng lặp sẽ in ra dãy số Fibonacci từ chỉ số 0 đến 5, chẳng hạn: "0 1 1 2 3 5".

Biến tĩnh trong đệ quy

Biến tĩnh (static variable) trong đệ quy đóng vai trò vô cùng quan trọng, giúp chúng ta giải quyết một số vấn đề mà các biến cục bộ thông thường không thể làm được.

Ý nghĩa:

Tồn tại suốt vòng đời của chương trình: Khác với các biến cục bộ bị hủy bỏ khi hàm kết thúc, biến tĩnh được khởi tạo một lần duy nhất khi chương trình bắt đầu và tồn tại cho đến khi chương trình kết thúc.

Giữ giá trị giữa các lần gọi hàm: Mỗi lần hàm đệ quy được gọi, biến tĩnh sẽ giữ nguyên giá trị của lần gọi trước đó. Điều này cho phép chúng ta "nhớ" những gì đã xảy ra trong các lần gọi trước, và sử dụng thông tin đó để tính toán kết quả cho lần gọi hiện tại.

Ví dụ 7: Sử dụng đệ quy để giải bài toán Tháp Hà Nội

Bài toán Tháp Hà Nội là một bài toán kinh điển trong khoa học máy tính, thường được dùng để minh họa cho khái niệm đệ quy. Mục tiêu là di chuyển tất cả các đĩa từ cột nguồn (Source) sang cột đích (Destination) với sự trợ giúp của cột trung gian (Auxiliary).

Cách giải bằng đệ quy:

↳ Ý tưởng chính là chia bài toán lớn thành các bài toán con nhỏ hơn, tương tự.

Theo các quy tắc sau:

↳ Chỉ di chuyển một đĩa một lần.

↳ Một đĩa chỉ có thể được đặt lên một đĩa lớn hơn hoặc lên một cột trống.

↳ Đĩa lớn hơn không thể đặt lên đĩa nhỏ hơn.

Chia nhỏ bài toán:

↳ Để di chuyển n đĩa từ cọc A sang cọc C, ta thực hiện các bước sau:

↳ Di chuyển n-1 đĩa trên cùng từ cọc A sang cọc B (để lộ ra đĩa lớn nhất ở dưới cùng của cọc A).

↳ Di chuyển đĩa lớn nhất từ cọc A sang cọc C.

↳ Di chuyển n-1 đĩa từ cọc B sang cọc C.

Điều kiện dừng:

↳ Khi chỉ còn 1 đĩa, ta di chuyển trực tiếp đĩa đó sang cọc đích.

public class TowerOfHanoi {
    public static void moveTower(int numDisks, char Nguon, char TrungGian, char Dich) {
        // Bước 1: Điều kiện dừng: Nếu chỉ còn 1 đĩa, di chuyển trực tiếp
        if (numDisks == 1) {
            System.out.println("Di chuyển đĩa 1 từ cột " + Nguon + " sang cột " + Dich);
            return;
        } else {
            // Bước 2: Di chuyển n-1 đĩa từ cột nguồn sang cột trung gian
            moveTower(numDisks - 1, Nguon, Dich, TrungGian); 
            // Ví dụ: moveTower(3 - 1, 'A', 'C', 'B') -> moveTower(2, 'A', 'C', 'B')
            
            // Bước 3: Di chuyển đĩa lớn nhất từ cột nguồn sang cột đích
            System.out.println("Di chuyển đĩa " + numDisks + " từ cột " + Nguon + " sang cột " + Dich);
            // Ví dụ: Di chuyển đĩa 3 từ cột A sang cột C
            
            // Bước 4: Di chuyển n-1 đĩa từ cột trung gian sang cột đích
            moveTower(numDisks - 1, TrungGian, Nguon, Dich); 
            // Ví dụ: moveTower(2, 'B', 'A', 'C')
        }
    }

    public static void main(String[] args) {
        int numDisks = 3; // Số lượng đĩa
        // Gọi hàm với 3 đĩa, từ cột A sang cột C với cột B là trung gian
        moveTower(numDisks, 'A', 'B', 'C');
        
    }
}

Phân tích chi tiết cách nó hoạt động nhé:

Điều kiện dừng (Base case):

↳ Nếu (numDisks == 1): Khi chỉ còn 1 đĩa, di chuyển trực tiếp từ Nguon sang Dich.

Bước đệ quy (Recursive call):

↳ Bước 1: moveTower(numDisks - 1, Nguon, Dich, TrungGian): Di chuyển n-1 đĩa từ Nguon sang TrungGian, sử dụng Dich làm cột trung gian.

↳ Bước 2: moveTower(numDisks - 1, TrungGian, Nguon, Dich): Di chuyển n-1 đĩa từ TrungGian sang Dich, sử dụng Nguon làm cột trung gian.

Phương thức main:

↳ Gọi hàm moveTower: với số đĩa là 3, A là cột nguồn, B là cột Trung gian và C là cột đích.

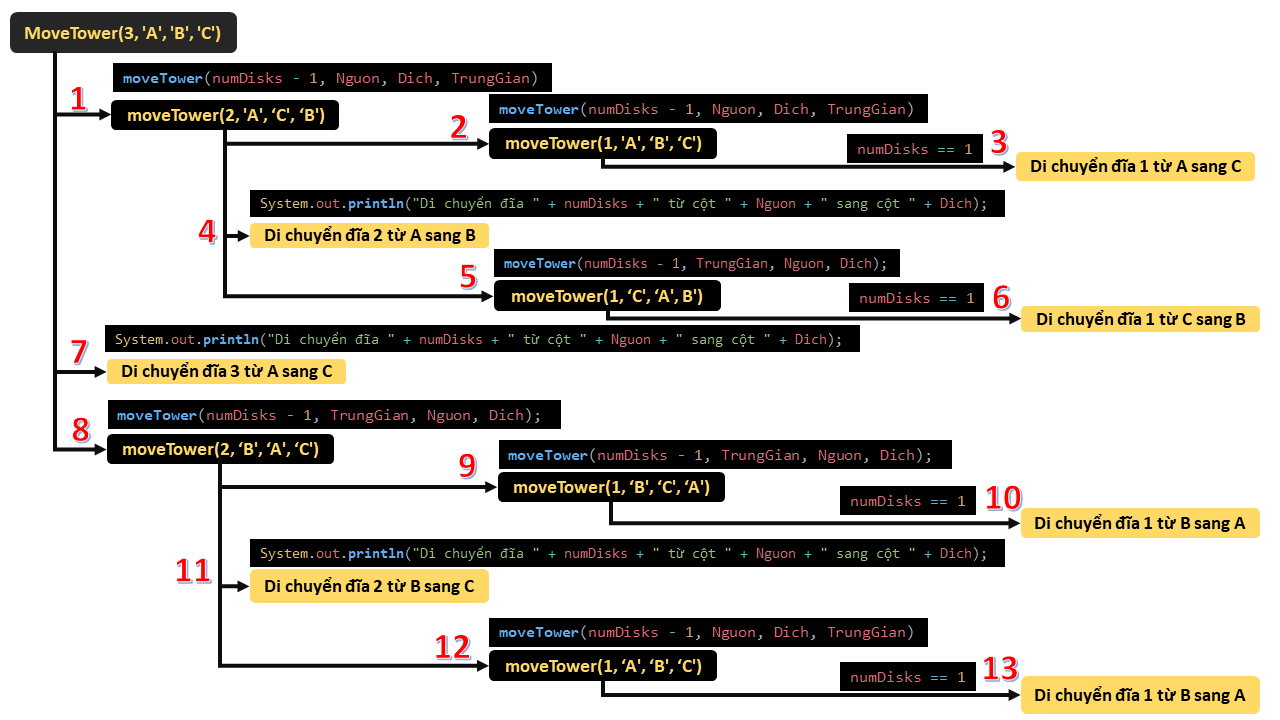
Ví dụ minh họa với moveTower(3, 'A', 'B', 'C') Quá trình thực hiện sẽ như sau:

Gọi hàm ban đầu:

↳ moveTower(3, 'A', 'B', 'C')

↳ numDisks = 3 (3 đĩa)

↳ Nguon = 'A' (Cột nguồn là A)

↳ TrungGian = 'B' (Cột trung gian là B)

↳ Dich = 'C' (Cột đích là C)

(1) Đệ quy bước 1 lần 1:

↳ moveTower(numDisks - 1, Nguon, Dich, TrungGian) -> moveTower(2, 'A', 'C', 'B')

↳ numDisks = 2 (2 đĩa)

↳ Nguon = 'A' (Cột nguồn là A)

↳ TrungGian = 'C' (Cột trung gian là C)

↳ Dich = 'B' (Cột đích là B)

(2) Đệ quy bước 1 lần 2:

↳ moveTower(numDisks - 1, Nguon, Dich, TrungGian) -> moveTower(1, 'A', 'B', 'C')

↳ numDisks = 1 (1 đĩa)

↳ Nguon = 'A' (Cột nguồn là A)

↳ TrungGian = 'B' (Cột trung gian là B)

↳ Dich = 'C' (Cột đích là C)

(3) Điều kiện dừng:

↳ numDisks = 1, di chuyển đĩa 1 từ Nguon sang Dich

↳ System.out.println("Di chuyển đĩa 1 từ cột A sang cột C")

(4) Quay lại đệ quy bước 1 lần 1:

↳ moveTower(numDisks - 1, Nguon, Dich, TrungGian) -> moveTower(2, 'A', 'C', 'B')

↳ numDisks = 2 (2 đĩa)

↳ Nguon = 'A' (Cột nguồn là A)

↳ TrungGian = 'C' (Cột trung gian là C)

↳ Dich = 'B' (Cột đích là B)

↳ System.out.println("Di chuyển đĩa 2 từ cột A sang cột B")

(5) Tiếp tục sử dụng đệ quy Bước 2:

↳ moveTower(numDisks - 1, TrungGian, Nguon, Dich) -> moveTower(1, 'C', 'A', 'B')

↳ numDisks = 1 (1 đĩa)

↳ Nguon = 'C' (Cột nguồn là C)

↳ TrungGian = 'A' (Cột trung gian là A)

↳ Dich = 'B' (Cột đích là B)

(6) Điều kiện dừng:

↳ numDisks = 1, di chuyển đĩa 1 từ Nguon sang Dich

↳ System.out.println("Di chuyển đĩa 1 từ cột C sang cột B")

(7) Quay lại Gọi hàm ban đầu:

↳ moveTower(3, 'A', 'B', 'C')

↳ numDisks = 3 (3 đĩa)

↳ Nguon = 'A' (Cột nguồn là A)

↳ TrungGian = 'B' (Cột trung gian là B)

↳ Dich = 'C' (Cột đích là C)

↳ System.out.println("Di chuyển đĩa 3 từ cột A sang cột C")

(8) Tiếp tục sử dụng đệ quy Bước 2:

↳ moveTower(numDisks - 1, TrungGian, Nguon, Dich) -> moveTower(2, 'B', 'A', 'C')

↳ moveTower(2, 'B', 'A', 'C')

↳ numDisks = 2 (2 đĩa)

↳ Nguon = 'B' (Cột nguồn là B)

↳ TrungGian = 'A' (Cột trung gian là A)

↳ Dich = 'C' (Cột đích là C)

(9) Tiếp tục sử dụng đệ quy bước 1:

↳ moveTower(numDisks - 1, Nguon, Dich, TrungGian) -> moveTower(1, 'B', 'C', 'A')

↳ numDisks = 1 (1 đĩa)

↳ Nguon = 'B' (Cột nguồn là B)

↳ TrungGian = 'C' (Cột trung gian là C)

↳ Dich = 'A' (Cột đích là A)

(10) Điều kiện dừng:

↳ numDisks = 1, di chuyển đĩa 1 từ Nguon sang Dich

↳ System.out.println("Di chuyển đĩa 1 từ cột B sang cột A")

(11) Quay lại tiếp tục sử dụng đệ quy bước 2:

↳ moveTower(numDisks - 1, TrungGian, Nguon, Dich) -> moveTower(2, 'B', 'A', 'C')

↳ moveTower(2, 'B', 'A', 'C')

↳ numDisks = 2 (2 đĩa)

↳ Nguon = 'B' (Cột nguồn là B)

↳ TrungGian = 'A' (Cột trung gian là A)

↳ Dich = 'C' (Cột đích là C)

↳ System.out.println("Di chuyển đĩa 2 từ cột B sang cột C")

(12) Tiếp tục sử dụng đệ quy bước 2:

↳ moveTower(numDisks - 1, TrungGian, Nguon, Dich) -> moveTower(1, 'A', 'B', 'C')

↳ numDisks = 1 (1 đĩa)

↳ Nguon = 'A' (Cột nguồn là A)

↳ TrungGian = 'B' (Cột trung gian là B)

↳ TDich = 'C' (Cột đích là C)

(13) Điều kiện dừng:

↳ numDisks = 1, di chuyển đĩa 1 từ Nguon sang Dich

↳ System.out.println("Di chuyển đĩa 1 từ cột A sang cột C")